| TEST di autovalutazione |
| 1 | Il flusso termico radiativo di un corpo nero a 200°C espresso in W/m2 è pari a (Kostante di Boltzmann 5,67 E-8): | ||
| A) | 2841 | ||
| B) | 90.72 | ||
| C) | 1134 | ||
| D) | 1000 | ||
| 2 | Due piani paralleli grigi, infinitamente estesi, sono mantenuti alle temperature costanti ed uniformi T1 = 500 K e T2 = 200 K (Kostante di Boltzmann 5,675,67 E-8). Sapendo che i coefficienti di assorbimento sono, rispettivamente, a1 = 0,4 e a2 = 0,7, il flusso specifico scambiato per irraggiamento è pari a: | ||
| A) | 34530 | ||
| B) | 1179 | ||
| C) | 878.9 | ||
| D) | 2417 | ||
| 3 | Due piani paralleli, infinitamente estesi, sono mantenuti alle temperature costanti ed uniformi T1 = 1000 K e T2 = 500 K (Kostante di Boltzmann 5,67 E-8). Sapendo che sono entrambi dei corpi neri, allora il flusso specifico scambiato per irraggiamento è pari a: | ||
| A) | 17718.75 | ||
| B) | 2835 | ||
| C) | 53156.2 | ||
| D) | 4252.5 | ||
| 4 | Una superficie di 2 m2 è alla temperatura di 1000 K e ha un coefficiente di assorbimento di 0,4. L'ambiente circostante (molto più grande della superficie) ha una temperatura di 300 K (Kostante di Boltzmann 5,67 E-8). Il flusso termico, espresso in kW, scambiato dalla supeficie con l'ambiente è pari a circa : | ||
| A) | 22.5 | ||
| B) | 112.5 | ||
| C) | 3.17 | ||
| D) | 45 | ||
| 5 | Su una superficie con coefficiente di assorbimento pari a 0,5 e temperatura pari a 400 K incide una potenza pari a 500 W/m2. (Kostante di Boltzmann 5,67 E-8). La Radiosità della superficie espressa in W/m2è pari a: | ||
| A) | 975.7 | ||
| B) | 475.7 | ||
| C) | 1225.7 | ||
| D) | 1701.5 | ||
| 6 | La radiosità di un corpo nero è uguale a: | ||
| A) | La radiosità di un corpo grigio | ||
| B) | La sua emissione globale | ||
| C) | La sua emissioe globale per il fattore di forma | ||
| D) | Il prodotto tra la costante di Bolzmann e la sua Temperatura | ||
| 7 | Si consideri una stanza a forma di cubo di lato L. Per la sua forma si può ipotizzare che la potenza radiativa emessa da ciascuna superficie non incide su se stessa. Allora la relazione che esprime la radiosità di ciascuna superficie può essere espressa come: | ||
| A) | 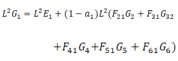 |
||
| B) | 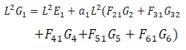 |
||
| C) | 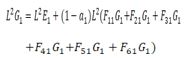 |
||
| D) | 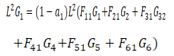 |
||
| 8 | Su una superficie incide una potenza radiativa di 400 W/m2. La superficie si comporta come un corpo grigio ed è in equilibrio termico a una temperatura di 350 K. Noto il suo coefficiente di riflessione, pari a 0,4, allora la sua radiosità espressa in W/m2, è pari a (Kostante di Boltzmann 5,675,67 E-8: | ||
| A) | 580.3 | ||
| B) | 670.5 | ||
| C) | 1090.8 | ||
| D) | 1010 | ||
| 9 | Sia il corpo 1 una piccola sfera al centro di una seconda sfera cava (Corpo 2). Se il Fattore id forma F21 è uguale a 0,4 allora il fattore di Forma F22 è uguale a: | ||
| A) | 1 | ||
| B) | 0 | ||
| C) | 0.4 | ||
| D) | 0.6 | ||
| 10 | Si consideri una stanza a forma di cubo di lato L=2m con le superfici assimilabili a dei corpi neri. La temperatura della supeficie A1 (base del cubo) sia pari a 1000 K mentre le altre superfici siano a 500 K. Considerando che inu cubo i fatttri di vista tra due superfici qualsiasi è pari a 0,2 (F11=0). La potenza radiativa scambiata dalla superficie 1 con le altre superfici è pari a kW: | ||
| A) | 1275.75 | ||
| B) | 1119.8 | ||
| C) | 1360.8 | ||
| D) | 212.6 | ||