| TEST di autovalutazione |
| 1 | Il fattore di vistta F12 tra due superfici A1 e A2 è dato da: | ||
| A) | Il rapporto tra l’energia che la superficie A1 emette e che raggiunge la Superficie A2 e l’energia totale emessa dalla superficie A1 | ||
| B) | Il rapporto tra l’energia che la superficie A2 emette e che raggiunge la Superficie A1 e l’energia totale emessa dalla superficie A2 | ||
| C) | Il rapporto tra l'energia che emette la superficie A1 sulla quantità di energia che raggiunge la superficie A2 | ||
| D) | Il rapporto tra l'energia che emette la superficie A1 su l'Energia che emette la superficie A2 | ||
| 2 | Sia A1 una delle superfici interne ad una cavità chiusa formata da 4 supefici allora i fattori di forma possono essere sicuramente legati dalla seguente relzaione: | ||
| A) | F11+F12=F13+F14 | ||
| B) | F11+F12+F13+F14=1 | ||
| C) | F11+F12+F13+F14=0 | ||
| D) | (F11+F12)/(F13+F14)=1 | ||
| 3 | Sia A1 una delle superfici di una cavità chiusa. Se l'energia emessa da A1 non incide su sestessa allora: | ||
| A) | F11=F12 | ||
| B) | F11=1 | ||
| C) | F12=1 | ||
| D) | F11=0 | ||
| 4 | Sia A1 una delle superfici di una cavità chiusa. Separte dell'energia emessa da A1 incide anche su sestessa allora posso dire che la parte di energia emessa da A1 che incide sulle altre superfici è esprimibile secondo la seguente relazione: | ||
| A) | F11 | ||
| B) | 1-F11 | ||
| C) | F12=1 | ||
| D) | F11-1 | ||
| 5 | Si definisce radiosità: | ||
| A) | Il prodotto dell'area A per il'emissione totale E (A E) | ||
| B) | La quantità di potenza radiante incidente totale su un'unità di superficie | ||
| C) | La quantità di potenza radiante complessivamente emessa per unità di superficie | ||
| D) | La parte di energia incidente su una superficie che viene riflessa dalla superficie stessa | ||
| 6 | Siano due superfici A1 e A2 con una rispettiva Radiosità G1 e G2 ed Emissione globale E1 ed E2. Sia, inoltre, il coefficiente di riflessione delle due superfici rispettivamente r1 e r2. Allora le potenze radiante complessivamente emessa dalla superficie A1 può essere espressa come: | ||
| A) | A1G1=A2E2+A2 F21 G2 | ||
| B) | A1G1=A2E1+A2 F21 G1 | ||
| C) | A1G2=A1E1+A1 F21 G1 | ||
| D) | A1G1=A1E1+A2 F21 G2 | ||
| 7 | Si considerino due piani paralleli affacciati ed infinitamente estesi con coefficiente di riflessione ed assorbimento rispettivamnete r1,a1 e r2 a2. Valga l'ipotesi che le temperature e proprietà radiative delle due superfici siano uniformi. Le supefici siano inoltre perfettamente diffondenti e si comportino come corpi grigi cone emissione globale rispettivamente E1 e E2. In regime stazionario il flusso radiativo q2 assorbito dalla superficie 2 può essere espresso dalla seguente relazione: | ||
| A) | 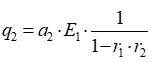 |
||
| B) | 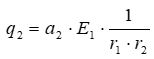 |
||
| C) | 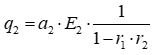 |
||
| D) | 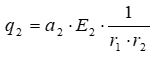 |
||
| 8 | Si considerino due piani paralleli affacciati di superficie A e con coefficiente di riflessione ed assorbimento rispettivamnete r1,a1 e r2 a2. Valga l'ipotesi che le temperature e proprietà radiative delle due superfici siano uniformi e sia trascurabile l'effetto dei bordi. Le supefici siano, inoltre, perfettamente diffondenti e si comportino come corpi neri cone emissione globale rispettivamente E1 e E2. In regime stazionario il flusso radiativo scambiato q(n) dalle due superfici è dato da: | ||
| A) | 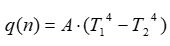 |
||
| B) | 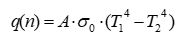 |
||
| C) | 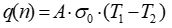 |
||
| D) | 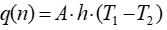 |
||
| 9 | Siano due superfici A1 e A2 con una rispettiva Radiosità G1 e G2 ed Emissione globale E1 ed E2. Sia, inoltre, il coefficiente di riflessione delle due superfici rispettivamente r1 e r2. Allora il flusso termico radiativo scambiato q dalla superficie A1 è dato dalla relazione: | ||
| A) | 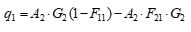 |
||
| B) | 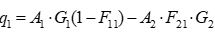 |
||
| C) | 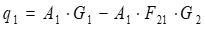 |
||
| D) | 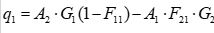 |
||
| 10 | Una sfera cava (Corpo 1) ha al suo centro una piccola sfera (Corpo 2). In base a tale geometria lo studente può plausibilmente ritenere che il fattore di forma F21: | ||
| A) | F21=1 | ||
| B) | F21=0 | ||
| C) | F21=0,5 | ||
| D) | F21=2 | ||