TEST di autovalutazione

1		Siano T1 e T2 (T1 maggiore di T2) le Temperature rispettvamente sulle due superfici di una parete piana (con spessore s e conducibilità λ). Allora, nel caso monodimensionale, il flusso in regime stazionario e in assenza di generazione di calore è dato da:
A)
B)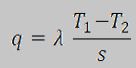
C)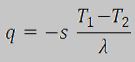
D)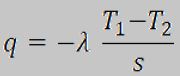

 

2		Siano T1 e T2 (con T1 maggiore di T2) le Temperature rispettvamente delle due superfici di una parete piana (con spessore s e conducibilità λ, nel caso monodimensionale). Allora la temperatura T variain funzione diella variabile spaziale x secondo la relazione:
A)
B)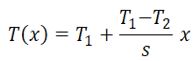
C)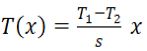
D)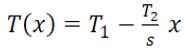

 

3		Si definisce Resistenza specifica per conduzione:
A)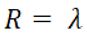
B)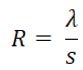
C)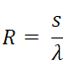
D)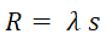

 

4		La Resistenza specifica per conduzione si misura in:
A)		W/m2 K
B)		M2 K/W
C)		W/m2
D)		W/m2

 

5		La resistenza specifica per conduzione totale di una parete con tre strati di spessore s1, s2 e s3 e con conducibilità termica rispettivamente λ1 , λ2 , λ3 è uguale a :
A)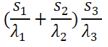
B)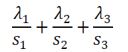
C)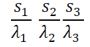
D)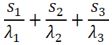

 

6		Parlando di conduzione: La resistenza di Contatto tra due pareti affiancate:
A)		Aumenta on la pressione che esercitano le due pareti reciprocamente (pressione di interfaccia)
B)		Aumenta con la temperatura della supeficie di contatto
C)		Aumenta con la durezza dei ateriali
D)		Diminuisce con la durezza dei materiali

 

7		Nel caso monodimensionale una parete di spessore s presenta al suo interno con generazione di calore H. Ipotizzando di essere in regime stazionario e parete isotropa e omogenea e con temperature identiche su entrambe le facciate, si può dire che la temperatura massima si trova:
A)		Su una delle due superfici
B)		In corrispondenza di s/2
C)		In corrispondenza di s/3
D)		Dipende dalla conducibilità della parete

 

8		L'equazione di Fourier in regime stazionario con generazione di calore si esprime tramite l'Equazione di Poisson che è data da:
A)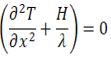
B)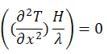
C)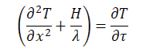
D)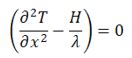

 

9		Dato un sistema in coordinate cilindriche. Sia un tubo di raggio interno r1 e raggio esterno r2 con conducibilità λ e di lunghezza L . Sia T1 la temperatura della superficie r1 e T2 la temperatura sulla superficie r2. La resistenza specifica per conduzione del tubo è data da:
A)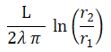
B)
C)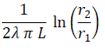
D)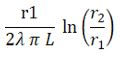

 

10		Sia una parete omogena e isotropa in un caso monodimensionale. Si consideri costante la differenza di temperature delle due superfici esterne. Nel caso di stato stazionari e assenza di generazione di calore, il flusso di calore che attraversa la parete:
A)		Diminuisce linearmente all'aumentare dello spessore
B)		Aumenta linearmente all'aumentare dello spessore
C)		Diminuisce in modo proporzionale al quadrato dello spessore
D)		Diminuisce proporzionalmente all'aumentare della conducibilità termica