| TEST di autovalutazione |
| 1 | La valutazione di una Espressione Booleana è rappresentata: | ||
| A) | Dalle Tavole di verità degli operatori logici presenti nell'Espressione | ||
| B) | Dalla Tavola di verità della funzione calcolata dall'Espressione | ||
| C) | Dal valore di verità assunto dalle variabili dell'Espressione | ||
| D) | Dal numero di variabili dell'Espressione che assumono valore "vero" | ||
| 2 | Due Espressioni Booleane sono equivalenti quando: | ||
| A) | Hanno la stessa lunghezza | ||
| B) | Hanno lo stesso numero di operatori AND, OR e NOT | ||
| C) | Le loro valutazioni forniscono Tavole di verità uguali | ||
| D) | Hanno le stesse variabili | ||
| 3 | Le proprietà degli operatori logici rappresentate da identità tra Espressioni Booleane consentono di: | ||
| A) | Sostituire l'AND con l'OR e il valore 0 con 1, e viceversa | ||
| B) | Modificare il valore di verità degli operatori logici | ||
| C) | Determinare le Tavole di verità degli operatori logici | ||
| D) | Trasformare una Espressione Booleana in un'altra equivalente | ||
| 4 | La forma canonica Somma di Prodotti e data da: | ||
| A) | Un AND di OR | ||
| B) | Un OR di AND tale che ogni AND contiene tutte le variabile in forma normale o complementata | ||
| C) | Un OR di AND | ||
| D) | Un AND di OR tale che ogni OR contiene tutte le variabile in forma normale o complementata | ||
| 5 | Un mintermine è: | ||
| A) | Una funzione la cui tavola di verità contiene un solo valore 1, data dall'AND di tutte le variabili in forma normale o complementata | ||
| B) | Una funzione di una sola variabile binaria | ||
| C) | Una funzione la cui tavola di verità contiene un solo valore 0, data dall'OR di tutte le variabili in forma normale o complementata | ||
| D) | La negazione di un AND di variabili Booleane | ||
| 6 | La forma canonica Prodotto di Somme e data da: | ||
| A) | Un OR di AND | ||
| B) | Un AND di OR tale che ogni OR contiene tutte le variabile in forma normale o complementata | ||
| C) | Un AND di OR | ||
| D) | Un OR di AND tale che ogni AND contiene tutte le variabile in forma normale o complementata | ||
| 7 | Un Maxtermine è: | ||
| A) | Una funzione la cui tavola di verità contiene un solo valore 0, data dall'OR di tutte le variabili in forma normale o complementata | ||
| B) | Una funzione che assume tutti i valori del Dominio dell'Algebra di Boole | ||
| C) | Una funzione la cui tavola di verità contiene un solo valore 1, data dall'AND di tutte le variabili in forma normale o complementata | ||
| D) | La negazione di un OR di variabili Booleane | ||
| 8 | La proprietà dell'insieme di opertatori AND, OR, NOT di essere funzionalmente completo significa che: | ||
| A) | Ogni Espressione Booleana che contiene questi operatori può essere valuta | ||
| B) | Tutti questi operatori possono essere valutati mediante Tavole di verità | ||
| C) | Le tavole di verità di questi operatori contengono almeno un valore diverso da 0 | ||
| D) | Data una qualunque funzione Booleana si può determinare una Espressione Booleana in cui figurano solo gli operatori AND, OR, NOT, e la cui valutazione è uguale alla funzione data | ||
| 9 |
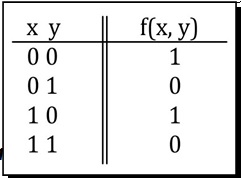 La forma canonica Somma di Prodotti della funzione Boleanna rappresentata dalla Tavola di verità in figura è data: |
||
| A) | 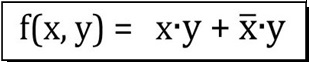 Dall'Espressione Booleana in figura |
||
| B) | 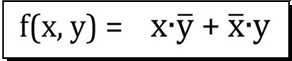 Dall'Espressione Booleana in figura |
||
| C) | 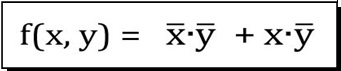 Dall'Espressione Booleana in figura |
||
| D) | 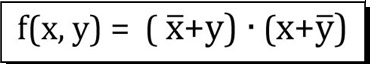 Dall'Espressione Booleana in figura |
||
| 10 |
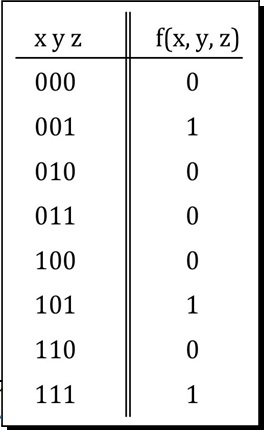 La forma canonica Somma di Prodotti della funzione Boleanna rappresentata dalla Tavola di verità in figura è data: |
||
| A) | 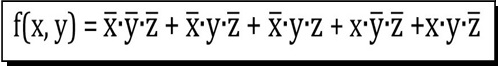 Dall'Espressione Booleana in figura |
||
| B) | 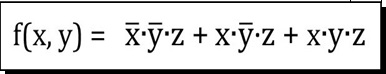 Dall'Espressione Booleana in figura |
||
| C) | 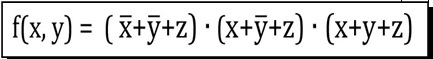 Dall'Espressione Booleana in figura |
||
| D) | 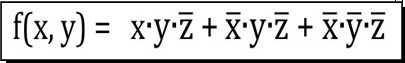 Dall'Espressione Booleana in figura |
||