| TEST di autovalutazione |
| 1 | L'espressione della distanza euclidea tra un punto x e un punto P di coordinate (a,b) è: | ||
| A) | 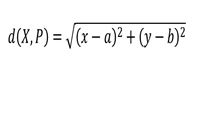 |
||
| B) |  |
||
| C) | 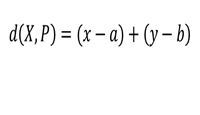 |
||
| D) | 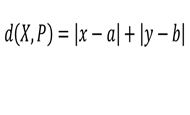 |
||
| 2 | Il metodo dei costi di trasporto proporzionali alla distanza euclidea è adatto in caso di: | ||
| A) | Spostamenti di persone all'interno di un edificio | ||
| B) | Viabilità in aree urbane | ||
| C) | Movimentazione di carrelli elevatori nei corridoi tra le scaffalature di un magazzino | ||
| D) | Tracciati di tubazioni | ||
| 3 | La formulazione del gravity problem è: | ||
| A) | 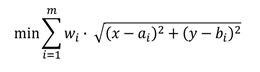 |
||
| B) | 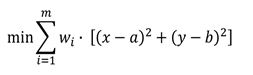 |
||
| C) | 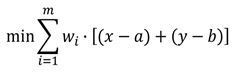 |
||
| D) | 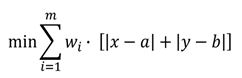 |
||
| 4 | Le coordinate ottime (x*, y*) individuate con il gravity problem si possono interpretare come: | ||
| A) | La media pesata del quadrato delle coordinate dei punti noti | ||
| B) | La media delle coordinate dei punti noti | ||
| C) | La media del quadrato delle coordinate dei punti noti | ||
| D) | La media pesata delle coordinate dei punti noti | ||
| 5 | Le linee isocosto nel gravity problem sono: | ||
| A) | Linee chiuse spezzate | ||
| B) | Rette | ||
| C) | Circonferenze concentriche nel punto di ottimo (x*,y*) | ||
| D) | Circonferenze concentriche nel punto noto con peso maggiore | ||
| 6 | Nel caso in cui l'ubicazione ottima (x*,y*) individuata risolvendo il gravity problem non sia disponibile: | ||
| A) | Ci si sposta nell'ubicazione disponibile più vicina in linea retta al punto di ottimo | ||
| B) | Ci si sposta presso il punto noto con peso maggiore | ||
| C) | Ci si sposta presso il punto noto con peso minore | ||
| D) | Ci si sposta lungo la congiungente il punto di ottimo e il punto noto con peso maggiore | ||
| 7 | Il metodo della mediana consente: | ||
| A) | Minimizzare la distanza media pesata delle distanze del punto noto più vicino e di quello più lontano dall’ubicazione incognita | ||
| B) | Minimizzare la media pesata delle distanze tra i punti noti e l’ubicazione incognita | ||
| C) | Minimizzare la distanza (pesata) tra punto noto più lontano e l’ubicazione incognita | ||
| D) | Minimizzare la distanza (pesata) tra punto noto più vicino e l’ubicazione incognita | ||
| 8 | Il metodo del costo consente: | ||
| A) | Minimizzare la distanza media pesata delle distanze del punto noto più vicino e di quello più lontano dall’ubicazione incognita | ||
| B) | Minimizzare la media pesata delle distanze tra i punti noti e l’ubicazione incognita | ||
| C) | Minimizzare la distanza (pesata) tra punto noto più lontano e l’ubicazione incognita | ||
| D) | Minimizzare la distanza (pesata) tra punto noto più vicino e l’ubicazione incognita | ||
| 9 | Applicando il metodo della mediana si sceglie: | ||
| A) | Il vertice con valore minore della somma delle distanze pesate dagli altri vertici | ||
| B) | Il vertice con valore minore del massimo delle distanze pesate dagli altri vertici | ||
| C) | Il vertice con valore minore del minimo delle distanze pesate dagli altri vertici | ||
| D) | Il vertice con valore maggiore della somma delle distanze pesate dagli altri vertici | ||
| 10 | Applicando il metodo del centro si sceglie: | ||
| A) | Il vertice con valore minore della somma delle distanze pesate dagli altri vertici | ||
| B) | Il vertice con valore minore del massimo delle distanze pesate dagli altri vertici | ||
| C) | Il vertice con valore minore del minimo delle distanze pesate dagli altri vertici | ||
| D) | Il vertice con valore maggiore della somma delle distanze pesate dagli altri vertici | ||